
吴振德先生
数学家——吴振德先生
吴振德先生1933年7月12日出生于浙江省定海县,1955年毕业于北京大学数学力学系,后在北京大学数学系任教。1958年初调入石家庄师范学院(河北师范大学前身)数学系工作。任河北师范大学数学与信息科学学院教授、基础数学博士生导师,兼任四川大学基础数学博士生导师。
先生聪慧豁达,思路敏捷过人,从小就对数学特别着迷。上初中时就开始自学高中课程,上高中时便开始自学大学课程,以致高考时填报的志愿全都是数学系。在北京大学数学力学系学习期间,他是班里的佼佼者,深得著名数学家江泽涵、廖山涛先生的赏识。20世纪50年代风华正茂的吴振德先生经常参加江泽涵先生领导的数学讨论班,为以后的研究工作打下了良好的基础。
先生始终倡导严谨认真、精益求精的学风。他凭着自己的聪明才智,更凭着不懈的追求和不屈的毅力,在拓扑学研究领域取得了累累硕果。从教50年来在《中国科学》、《科学通报》、《数学学报》等高水平学术期刊发表学术论文40余篇。仅1981年一年就在《数学学报》发表拓扑学论文6篇。解决了我国著名数学家吴文俊教授在1956年提出的若干个问题中的三个问题,解决了著名拓扑学家Steenrod教授所提出的若干个问题中的一个,回答了拓扑学家Stong教授所提的一个问题,在国内外引起反响。我国著名拓扑学研究专家、南开大学数学系教授、博士生导师周学光先生在概括了吴振德先生的研究成果后评价说:“所有这些都是国内和国际上领先的工作,在理论上具有重要的意义。”吉林大学数学系教授、博士生导师孙以丰先生对吴振德先生的研究成果评价说:“无论从其深度、难度以及内容之丰富多彩性来看,均属于国际先进水平。”(见《治学与做人》,1999,河北教育出版社)。中国科学院院士、原北京大学数学科学学院院长姜伯驹教授在河北省重点学科建设论证意见中写道:“河北师范大学的基础数学专业学术力量雄厚,在河北省是领先的。特别是在拓扑学方面,在吴振德教授的指导下,在现代拓扑学这个领域内成为全国范围内六七个主要研究集体之一,在难度大的课题上取得高水平的成果,并且培养了一批年轻人才输送各地。” 吴振德先生的研究成果也得到了祖国和人民的高度赞誉,1982年他获得河北省科技成果三等奖,1983年7月晋升为教授,1984年经国家人事部批准为国家级有突出贡献的中青年专家,1991年起享受国家的政府特殊津贴,1991年获河北省科技进步二等奖,1992年被批准为河北省首批省管优秀专家,1993年获曾宪梓教育基金会高师院校教师二等奖,同年经国务院学位委员会通过为基础数学博士生导师,1996年获得河北省科技进步一等奖。
先生热爱教育事业,十分重视数学基础的培养,强调“数学功底”和“数学素养”的教育,并积极地贯穿在教学实践之中。先生在承担繁重的研究生指导任务的同时,坚持为本科生上课。先后为本科生开设了数学分析、解析几何、高等几何、代数拓扑学、点集拓扑学、高中数学竞赛解题指导等近十门课程。他经过多年的探索和研究总结出“四步教学法:讲解要领来源-提出带有启发性的新问题-举出具体实例-运用新知识解决问题”,很好地体现了他的数学教育思想。先生1983年起开始招收硕士研究生,1994年开始招收和培养博士研究生。先后为研究生开设了纤维丛、同调代数等十门课程。先生总是把自己的最新成果讲出来,引导学生把眼光放在本领域的最前沿,鼓励学生多与外界交流,大胆设想,小心求证,勤于思考,独立研究。先生培养的学生已遍布河北、内蒙古、广西、广东一些院校,在先生的带领下已形成代数拓扑界一支重要的新生力量。
吴先生在河北师范大学教学科研第一线辛勤耕耘了48个春秋,对河北师大,特别是数学系的学科建设、学风建设影响巨大。河北师大的数学学科由弱到强,发展为今天的河北省重点学科,并拥有基础数学博士学位授权点;数学系由小到大,发展为今天拥有170多名教职工、3000多名本科生和硕士、博士研究生的数学与信息科学学院,无不蕴含着吴振德先生的沥沥心血。1962年为贯彻高教六十条,学校下力量抓青年教师的进修培养,年仅29岁的吴振德先生主动组织起几何组的青年教师,利用课余时间开设拓扑学研讨班,直到“文革”受到冲击而不得不暂停下来。1978年先生刚一“解放”就又组织起拓扑讨论班,每周定期上课,几十年如一日默默耕耘。在先生的鼓励、督促、指导下,几何教研室人才辈出,全院学风日盛。先生还经常开设现代数学前沿讲座,向青年教师传递国际数学研究的最新动向,引领青年人勇攀科学高峰,使许多年轻教师在日后的教学、科研上脱颖而出。先生诲人不倦、甘为人梯,总是尽力为青年教师提供发挥才能的舞台,善于看到他们的成绩,予以热情鼓励。正是由于先生无私奉献的园丁精神和在工作中的突出表现,1989年获得了全国教育系统劳动模范称号和“人民教师”奖章。
1990年12月,先生被国家教委聘任为“首届高等学校数学与力学教学指导委员会委员”,先后担任过河北高校职称评审数学学科组副组长,河北师范大学职称评审委员会副主任,《数学研究与评论》编委,河北师范大学学报(自然科学版)主编、编委会顾问,并一直担任着《数学季刊》编委。历任河北省数学会副理事长、理事长,第六、七、八届河北省人大代表,第八届河北省人大常委。
先生德高望重,为人忠厚诚恳,做人、做事从来不拿架子,始终把自己看作是河北师范大学的普通一员。1985年先生加入中国共产党,努力追求全心全意为人民服务的最高境界,淡泊名利、虚怀若谷、胸怀坦荡、平易近人,深受全校师生的崇敬和爱戴。
吴振德先生在代数拓扑和微分拓扑研究中所取得的成就主要有以下几方面:
1. 示嵌类方面
早已知道n维有限单纯复形一定能嵌入2n+1维欧氏空间内,问题是如何找出:“n维有限单纯复形能嵌入2n维欧氏空间的充要条件。”
吴文俊教授解决了这一难题,引进了示嵌类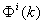 并且还证明了以下的结果:
并且还证明了以下的结果:
定理 若 是一个可剖分n维闭微分流形,且有
是一个可剖分n维闭微分流形,且有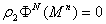 ,则有
,则有

定理 若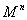 是一个n维可剖分闭微分流形,且有
是一个n维可剖分闭微分流形,且有 则有
则有

吴文俊教授在1956年的一次报告会上,提出了若干个问题,其中有两个问题如下:
(i) 是否存在一个n维闭微分流形,它对(2)成立,但(1)不成立?
(ii) 是否存在一个n维闭微分流形,它对(1)成立,但 ?
?
文[1],[2]证明了
定理 若 是一个n维可剖分的闭流形,则
是一个n维可剖分的闭流形,则 的充要条件为
的充要条件为
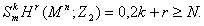
这个定理的必要部分为吴文俊教授已经证明的,由于这个结果,说明了(i),(ii)中的n维闭微分流形是不存在的。
这个结果被写入吴文俊教授的名著“可剖形在欧氏空间中的实现问题”中的第七章。
利用上述定理,可以证明以下结论:
定理 (1)当 为n维可剖分的闭流形,
为n维可剖分的闭流形, 时,则有
时,则有
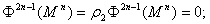
(2)当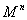 为 n维可剖分的可定向的闭流形,
为 n维可剖分的可定向的闭流形, 时,则有
时,则有
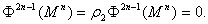
上述问题也是吴文俊教授在1956年的报告会中提出的一个问题。
2. 上同调运算方面
p为素数时,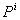 为Steenrod p-power,
为Steenrod p-power,
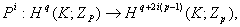
当 p=2 时,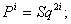
p=2时,ПОHTPЯГNH运算

当p为奇数时,Thomas推广为
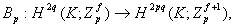
1957年,N.E.Steenrod提出了若干个问题,其中之一为“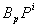 是否为可分解的?”,也可以推广为
是否为可分解的?”,也可以推广为 是否为可分解的?
是否为可分解的?
利用Adam关于Streenrod p-power的关系知除
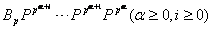 以外都是可分解的,在文[3]中,证明了
以外都是可分解的,在文[3]中,证明了
定理 运算 是不可分解的。
是不可分解的。
这就解决了所提出的问题。
3. 微分映射奇点方面
H.Whitney首先研究了从k维微分流形到2k维和(2k-1)维实向量空间的光滑映射的奇点问题。以后,他又研究了从2维向量空间到2维向量空间的光滑映射的奇点问题。ПОHTPЯГNH和ДObpyшNHa用另外的方法研究了从k维紧微分流形到2k维,2k-1维,2k-2维实向量空间的光滑映射的奇点问题,文[4],[5]继续延用了ПОHTPЯГNH的方法,研究了从k维紧致微分流形到2k-n维实向量空间的光滑映射的奇点问题,k≥2N-2,以及从k维紧致微分流形到二维实向量空间的光滑映射的奇点问题。
4. 拓扑K—理论方面
Atiyah和Hirzebruch利用向量丛的加法与乘法定义了一种广义同调群KO—群和K—群。文[6],[8],[12],[15],计算了Stiefel流形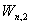 ,
,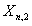 ,
, 的KO—群,透镜空间
的KO—群,透镜空间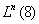 的KO—环,Stiefel流形
的KO—环,Stiefel流形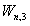 ,
,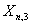 的KO—群。
的KO—群。
Adams在“On the groups J(x),Ⅰ—Ⅳ”中引进了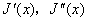 并证明了
并证明了
 。
。
Quillen证明了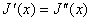 ,从而有
,从而有
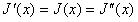 。
。
文[6],[7],[8],[9],[10],[11],[12],[13],[14]利用了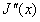 的可计算性,计算了
的可计算性,计算了
(i) Stiefel流形 ,
,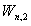 ,
,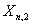 的J群。
的J群。
(ii) 透镜空间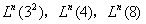 的J群。
的J群。
(iii) Dold流形D(m,n),n≤5的J群。
(iv) 复射影空间 ,
, ,四元射影空间
,四元射影空间 ,q=3,4,5的J群。
,q=3,4,5的J群。
(v) 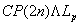 (p为素数)的J群。
(p为素数)的J群。
5. 等变协边理论方面
R.Thom引进了一种广义同调理论——协边理论,Conner和Floyd考虑了群G在流形上的作用,而出现了等变协边理论。
当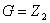 时,这是最简单的情形,也是内容最丰富的情形,称为带对合的流形。
时,这是最简单的情形,也是内容最丰富的情形,称为带对合的流形。
(i) R.E.Stong在1973年提出了下面的问题,如果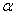 为n维上协边类,又存在一个代表元M
为n维上协边类,又存在一个代表元M ,且有一个对合在上作用,使这个对合的不动点集为n-r维闭流形,所有这样的
,且有一个对合在上作用,使这个对合的不动点集为n-r维闭流形,所有这样的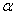 构成的集合记作J
构成的集合记作J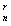 。记
。记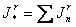 ,要找出
,要找出 的充要条件。稍后,r=2,3,4,5,6,7,8均已决定,在文[20],[25]决定了
的充要条件。稍后,r=2,3,4,5,6,7,8均已决定,在文[20],[25]决定了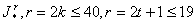 。
。
(ii) 1978年Kosniowski和Stong提出一个问题,对于给定的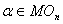 (n维上协边类),β
(n维上协边类),β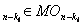 满足Euler示性数的条件:
满足Euler示性数的条件: ),是否存在α的一个代表元
),是否存在α的一个代表元 ,以及在
,以及在 上的一个对合T,使T的不动点集为
上的一个对合T,使T的不动点集为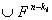 ,且有[
,且有[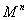 ]=
]= ,[
,[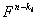 ]=
]=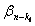 。文[19],[24],[29]回答了这个问题:当
。文[19],[24],[29]回答了这个问题:当 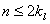 (
(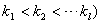 时,可以举出不少例子说明此时不可能,当
时,可以举出不少例子说明此时不可能,当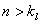 时上述性质是成立的。
时上述性质是成立的。
(iii)  为正整数,
为正整数,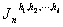 为
为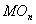 内具有下述性质的n维上协边类α的集合,它的一个代表元
内具有下述性质的n维上协边类α的集合,它的一个代表元 ,以及在
,以及在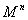 的一个对合T,使T的不动点集
的一个对合T,使T的不动点集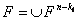 ,文[23],首次讨论这种情形,并在文[30],[33],决定了
,文[23],首次讨论这种情形,并在文[30],[33],决定了 (
(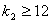 )。
)。
(iv) Capobianco讨论了带对合流形(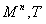 )的不动点集为
)的不动点集为 的情形,并对
的情形,并对 的情形做了猜测,文[16]证明了这个猜测。
的情形做了猜测,文[16]证明了这个猜测。
(v) 对于给定的( ),要决定它所有协边类的结果比较少,文[28],[32],决定了
),要决定它所有协边类的结果比较少,文[28],[32],决定了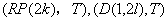 的协边类
的协边类 的情形。
的情形。
(i)  为
为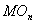 内具有下述性质的协边类所组成的集合:它的一个代表元
内具有下述性质的协边类所组成的集合:它的一个代表元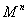 ,在
,在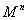 上有
上有 作用,使它的不动点集为n-r维闭流形。R.J.Shaker首先决定了
作用,使它的不动点集为n-r维闭流形。R.J.Shaker首先决定了 ,
, ,文[36],[40]已决定
,文[36],[40]已决定 ,
,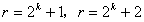 。以后还决定了
。以后还决定了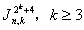 ,
, 。
。
(ii) P.L.Q. Pergher首先首先讨论了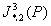 ,P=(1,1,1)情形。文[39]讨论了
,P=(1,1,1)情形。文[39]讨论了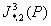 , p={(2,1,0),(2,0,1),(1,1,1)}情形(此问题为Pergher所提出);文[38]讨论了
, p={(2,1,0),(2,0,1),(1,1,1)}情形(此问题为Pergher所提出);文[38]讨论了 ,p={(2,0,2),(0,2,2),(2,2,0) }。
,p={(2,0,2),(0,2,2),(2,2,0) }。
(iii) P.L.Q Pergher证明了 时,有
时,有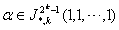 =0。文[39]推广到
=0。文[39]推广到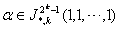 时,仍有
时,仍有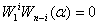 。
。
河北师范大学数学与信息科学学院
(执笔人:王运敏)
2004年6月16日
版权所有©2013河北师范大学校友会 冀ICP备18011017号-3
技术支持:载驰科技